How Can I Divide Greater Numbers Using A Standard Procedure

You've guided your class through most of the big units: addition, sectionalisation, subtraction, multiplication. Merely here'south some other tricky ane:

How to exercise long segmentation.

A 2012 written report published in Psychological Science institute that 5th graders' understanding of fractions and sectionalization could exist straight linked with how well they understood algebra in high school and performed in higher-level math classes — even after controlling for various socio-economic factors.No pressure, correct? If the thought of teaching long division gives you lot cold sweats and clammy palms, not to worry — we've washed all the work for you lot.

How to do long division in six steps

ane. Review

The first stride you should take is a step back.

For a fourth grade pupil, long sectionalisation is a complicated mix of different operations. In order to successfully acquire how to do long segmentation, they need to review these cardinal concepts.

According to a French study, "the representation and retrieval of mathematical facts from long-term retentiveness" is one of the most of import factors in determining a pupil'south future mathematical success. According to the same written report, long division is "a synthesis of all arithmetic knowledge."

Brand sure your students understand that multiplication is the product of repeated addition, and division is just the opposite — repeated subtraction.

Use base 10 blocks or money to reinforce place value and number sense. Program activities that enquire students to create "fact families" in order to brand certain students empathise how unlike functions collaborate.

Use multiplication games and other math games to go students excited nearly learning and to build math confidence earlier you keep going.

2. Kickoff elementary

Let's begin with a vocabulary lesson.There are lots of different parts in a long division equation. Brand certain your students know what they mean and how to identify them.

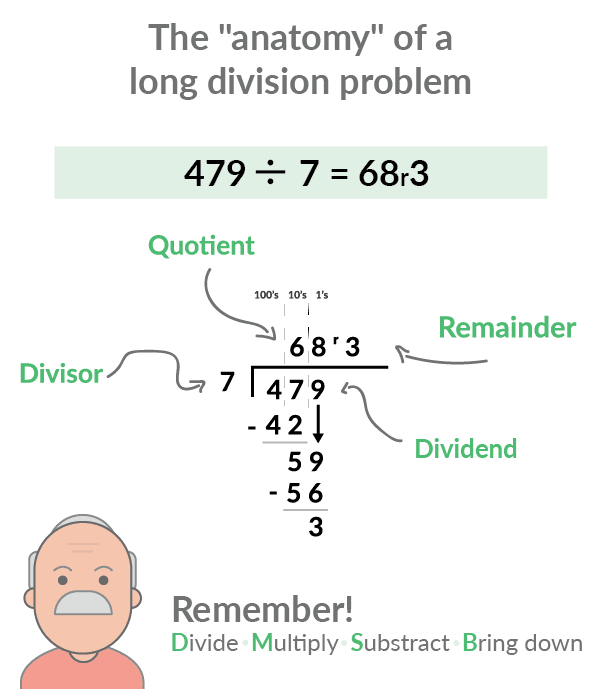
The dividend is the number on the right side of the equation, under the line. Information technology represents the corporeality being divided.

The divisor is the number on the left -- it'due south the i doing the dividing.

The quotient is the number on the top. It represents the respond, or the number of units in each place value once the equation has been completed.

The remainder is the number on the top right. Information technology represents the units left over that can't be evenly divided into the quotient.Commencement, innovate an equation that doesn't have whatsoever remainders so students tin can get used to the format and showtime understanding the new vocabulary they've simply learned:

Ask students how many times ii fits into four. This might be a tricky concept for them, then utilise the idea of sharing: If you want to share 4 objects between ii people, how many objects does each person go?

Once they come up with the correct answer, put 2 to a higher place 4. Then, repeat the step with the second digit in the dividend.

Use these simple equations to reinforce place value. Teach students that when they're request how many times ii can go into iv, they're actually asking how many times 2 goes into xl.

3. Residuum in the ones

Accept your students practise the footstep above until they're comfortable with the basic format. And then, it's time to move on.

Instead of jumping right into an equation with remainders, start with another object lesson. Split students into groups of three, 4 or six and give each grouping l cotton balls (or jelly beans, or pompoms, or marshmallows — whatever small object is accessible in your classroom).

Ask students to dissever the objects upward so each fellow member of the group has an equal number, then picket and wait.

Eventually, they'll understand they can't divide information technology evenly and in that location will always be some objects left over. That's where y'all come up in to save the day and explicate how to do long partitioning with remainders.

Kickoff, show students a trouble that has a remainder in the ones:

Now, begin with the tens cavalcade and piece of work through the trouble: 5 goes into 5 exactly once, so there's nada left there. But how many times does 5 go into 7, and what do you practice with the leftovers?

Show students the new steps:

Divide the ones column dividend past the divisor
Multiply the divisor by the quotient in the right place cavalcade
Subtract the product from the ones column

The number they're left with is the residuum. Make sure to model several problems equally a form then students can brainstorm to sympathize the steps and how to properly write their answers.

This is a good fourth dimension in the lesson to teach students how to cheque their answers. Have them multiply the divisor by the quotient and add the remainder — the answer should be the same as the dividend they started with.

4. Remainder in the tens

Now it'south fourth dimension for students to tackle problems where the divisor doesn't fit neatly into the tensorones column. The steps are more or less the same, except for one new add-on:

Separate the tens column dividend past the divisor
Multiply the divisor by the caliber in the tens identify column
Subtract the product from the divisor
Bring downwardsthe dividend in the ones column andecho.

Start with i-digit divisors and 2-digit dividends to keep things simple. Call up that this is a totally new concept for students, so take the time to model issues on the lath. Have a word nigh why the steps piece of work, and aid them understand how place value plays an important function in the process.

5. Innovate bigger numbers, gradually

So that'due south information technology. Or is it?

Let students get comfortable with the formula and work on smaller problems. As they develop confidence and begin to understand how to exercise long division, offset presenting them with bug that have a 3-digit dividend, then problems that have a two-digit divisor.

Remind students that the steps stay exactly the same no matter how big the problem is, and encourage them to use flake paper to "gauge-and-check" their multiplication equally they go. This is a expert spot to make certain that they're not struggling and that they completely understand the relationship that division has with place value and multiplication.

For a refresher, check out this video from Khan Academy:

six. How to do long division with decimals

If you've covered all your content in the beginning v steps, congrats! Have students keep practicing how to do long sectionalisation with big and small numbers, and keep reinforcing the relationship betwixt partitioning and other math concepts that they're learning.But the procedure isn't quite washed still — students demand to empathize how to do long division with decimals.To begin, get back to one of the fundamental concepts of division: place value. However, this fourth dimension yous'll be going backwards instead of forwards.

Have students solve a problem as they normally would. When they become to the pace where they would commonly stop with a residuum, accept them identify a decimal bespeak at the stop of the quotient and the divided, and write in several zeros after the dividend.

Take them go along regular partitioning steps for one or two places, bringing down the zeros.

Connect the decimal to fractions. Enquire them to convert the quotient, with the decimal, to an improper fraction. This should assistance them understand the human relationship betwixt fractions and place value, and tin be a good opportunity to go over fraction basics.

How to exercise long division (without doing long division)

Congratulations! Your unit is coming to an end, and you've successfully taught your students how to practice long segmentation.

Only did you know that there'south more than than one way to split big numbers? Teaching students other ways of checking their piece of work is an of import part of Mutual Cadre math standards and tin can improve student understanding of what long division really means in a given context.

Area models

Surface area models are a great way for visual learners to sympathise and conceptualize division while also enhancing number sense.

This method uses a grid to present the process of division as an expanse trouble: for example, 148÷4 would exist divided into a filigree that is 4 units high, 148 square units in area, and an unknown number of units wide.

Students break up the filigree into more manageable areas: 100 square units, 40 square units and 8 square units. 100÷iv is 25, 40÷4 is x, and 8÷iv is 2. Those numbers become on the top of the expanse model and tin be added up to reach the answer.

Fractional quotients

Similar to the area model, partial quotients encourage students to pause division questions down into "friendlier" chunks. Information technology helps students understand that division is finding how many times one number tin go into another number.

Ready the problem (in this example, 450÷23) like a long division equation. Have pupil students multiply the divisor past two and 5 to utilise as an piece of cake reference.

Ask how many times 23 goes into 400, simply don't look for the verbal closest number: get in an easy number to work with, like 230 (ten times). Subtract 230 from 450 and put the 10 on the right to keep runway of it.

Take the difference and decrease information technology from the dividend. The answer should be 220.

Ask how many times 23 goes into 220. 5 x 23 is 115, and then subtract that from 220 and tape the 5.

Proceed going, multiplying and subtracting until the final number is as well small. When you lot've reached that step, you've found your remainder! Add together upwardly the numbers in the right-hand cavalcade to find your quotient.

Partial quotients have a flexibility that long division doesn't. Long division needs to be done precisely, merely with fractional quotients it's possible to simply subtract the divisor from the dividend repeatedly and even so come up to the right answer.

Use this method to reinforce place value and the concept of sectionalisation equally repeated subtraction.

Long division activities

The best way for students to learn how to do long segmentation is to practice, practice, practice.

Hither's a listing of eight activities that volition get your class excited about long division and help them develop solid math skills.

1. Prodigy

Prodigy is a fun and engagingresource for in-class or at-domicile long partitioning practice. Students explore a world filled with run a risk, where success depends on correctly answering math questions.

Through the teacher dashboard, you tin deliver lesson-aligned content based on the grade, skill or educatee. So, students answer these questions in-game and provide you with real-time feedback on their learning and comprehension.

Encourage your students to practice all the math skills they've been learning in the classroom — including long division. Here's how you lot can use Prodigy to:

Reinforce in-class lessons
Differentiate math content
Conduct determinative assessments

Students play the engaging game-based platform, where they tin collect pets, proceed quests and battle with friends. And while they're having fun, you're helping them develop long division skills. It's a win for everyone!

2. Life-sized long division

Bring math to life with a easily-on long partitioning puzzle. Cutting out squares of colorful paper with all the numbers that students demand to solve a long division problem from start to cease. Apply masking tape to brand sectionalisation lines on the floor, and give students the numbered cards.

Starting with a given equation, have students lay out all the cards in the correct gild to solve the equation. This activity challenges students to boring down and call up about their steps, and it'due south particularly helpful for a class that's yet looking to principal the multiplication steps.

3. Long division bingo

Bingo is a classic for a reason. Each of the numbers on a educatee'southward sheet should match upwards to a question that you accept at the forepart of the classroom. Write the problem on the board, and so give students scratch paper and a chance to solve it and see if they accept it on their card. As e'er, the first student to fill upward a whole row, wins!

Challenge your students, only make sure you take enough time with this activity — some students might have problem solving problems chop-chop, and tin get frustrated or make mistakes if they're not able to keep up.

4. Math books

Boost literacy and math learning at the same time with fun books covering catchy math concepts. Utilize them to explain sectionalization and remainders to students in a fun and engaging manner, and even to cover more bones concepts earlier they showtime learning how to do long sectionalisation.

Some math books that encompass division include:

A Residue of Ane by Elinor J. Pinczes
Edible bean 13by Matthew McElligott
The Doorbell Rang by Pat Hutchins

v. Get creative

Long partitioning has lots of steps, and they have to exist washed in the correct order to get to the correct answer. Students can get confused or frustrated when they don't remember the steps, which negatively affects their math confidence and performance.

Challenge students to come up with their own unique fashion to remember how to do long sectionalization —divide, multiply, decrease and bring downward— to get the inventiveness flowing in your classroom.

Have them create a poster, song, mnemonic device or even a small skit that they tin can nowadays to their classmates. If they're invested in finding a way to call back the steps, they're more likely to learn chop-chop.

6. Long sectionalisation relays

Plow long division practice into a fun classroom game with long division relays. Divide your grade up into teams and make cards with long partition bug on them.

Line upward students in groups. Each group gets a card to first, and the first students consummate the beginning prepare of steps for the problem they accept.

When they're done, the second student looks for errors and continues the problem. If they finish the problem, they tin call for you to come check their work and trade the correct answer for a card with a new problem.

Keep going until every group has answered all their cards, and see which team wins!

7. Treasure chest

This activity is a fun fashion for your class to gloat finishing their unit of measurement on division. Get a few boxes and fill up them with a small care for anybody in the course can bask. Include a list of multiplication bug that students must solve in groups to "unlock" the box.

For an added challenge, make information technology a lawmaking: Have every caliber match upwardly to a letter so that students have to correctly decode a key phrase to open the box.

8. Worksheet generator

Worksheets are a tried-and-true staple of math class. Lucky for you, at that place are lots of websites that will practice the piece of work for you and generate a custom worksheet that will give your students the modify to do how to do long division. Here are a few of our favourites:

Helping with math
Math Aids
Worksheet genius

Concluding thoughts on didactics students how to do long division

The most important thing to remember when pedagogy students how to practice long sectionalisation is to not blitz through the material. Information technology's a big concept that'due south unlike from anything they've learned before, and some (if not all) of your students might struggle at first.If you need to, go back to simpler equations and some of the earlier steps that nosotros've outlined for y'all and work through them until your students feel confident. Keep on encouraging and challenging your students, and they'll be set to divide and conquer in no time!